Matematika kelas 8 persamaan garis lurus

dengan grediennya.

Bentuk umum persamaan garis lurus

                                                        y = mx + c
Keterangan :     m = gradien
   c =  konstanta

Persamaan garis dapat dinyatakan dalam berbagai bentuk dan variabel.

Contoh:
 y = 2x - 1 dan a = b + 2

A. Mencari Gradien (m)

Gradien (m) adalah nilai yang menyatakan kemiringan suatu garis.

1. Gradien Garis yang melalui dua titik A(x1, y1) dan B(x2, y2)

•  Gradien dari dua garis yang sejajar

Garis g sejajar dengan garis h. Jika gradien garis h adalah , dan gradien garis g adalah 
Maka

•  Gradien dari dua garis yang saling tegak lurus

2. Pada Grafik

• Ruas Garis

                         

     




       

• Melalui pusat koordinat

• Garis memotong kedua sumbu

        




3. Pada Persamaan Garis

Bentuk :         y = mx + c            → gradien = m

                       ax+by+c = 0       → gradien = (-a)/b
                        x/b+y/a  = 1        → gradien = (-a)/b

B. Membuat Persamaan Garis Lurus

• Persamaan garis lurus yang melalui sebuah titik (x1,y1) dan bergradien m

• Persamaan garis lurus yang melalui dua titik (x1,y1) dan (x2,y2)

     
atau

C. Membuat Grafik Garis Lurus

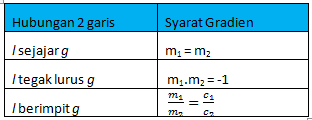
Salah satu cara membuat grafik garis lurus adalah mencari titik-titik potong pada sumbu x dan sumbu y. Gunakan tabel berikut

D. Hubungan Persamaan Garis dan Gradien

left;"> misal : garis l memiliki persamaan 

garis g memiliki persamaan

E. Sifat Persamaan Garis

1. Memiliki gradien m dan memotong sumbu Y dititik (0,c)

2. Jika m > 0, maka garis condong ke kanan ( naik)

    Jika m < 0, maka garis condong ke kiri (turun)

    Jika m = 0, maka garis mendatar sejajar sumbu X

3. Jika c > 0, maka titik potong dengan sumbu Y diatas sumbu X

    Jika c < 0, maka titik potong dengan sumbu Y dibawah sumbu X

    Jika c = 0, maka titik potongnya pada titik pusat koordinat

Contoh soal dan pembahasan :
1. Gradien garis yang melalui titik A(-1,3) dan B(7,-5) adalah....
A. 2
B. 1
C. 1/2
D. -1
pembahasan :



2. Gradien dari persamaan garis 2y = x - 3 adalah....
A. 2
B. 1
C. 1/2
D. -1
pembahasan :


3. Garis l sejajar dengan garis g yang memiliki persamaan 2x + 3y -8 = 0, gradien garis l adalah....
A. -2/3
B. -3/2
C. 2/3
D. 3/2
Pembahasan :

karena garis l sejajar garis g maka 

4. Persamaan garis yang memiliki gradien 3 dan melalui titik (-2,5) adalah....
A. y = 3x + 11
B. y = 3x - 11
C. y = 3x + 1
D. y = 3x - 1
pembahasan :

Persamaan garis lurus yang melalui titik (2,1) dan titik (-2,-7) adalah....

A. y = - 2x \= 5

B. y = 2x -3

C. y = 3x - 5

D. y = - 3x + 7

pembahasan :